
Josep M. Subirachs
Cuadrado mágico (escena del beso de Judas)
Escultura en piedra.
Fachada de la Pasión. Sagrada Familia. Barcelona |
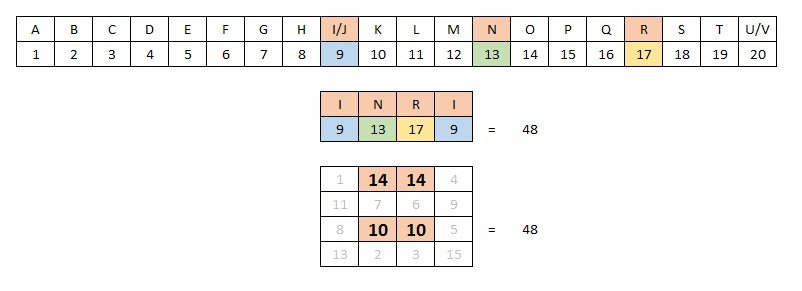
Comenzamos hoy con el cuadrado mágico de la Fachada de la Pasión de la Sagrada Familia de Barcelona, obra de Josep M. Subirachs. Los cuadrados mágicos son juegos matemáticos formado por una serie de números dispuestos dentro de una cuadrícula de tal manera que cualquier fila, columna o diagonal sume siempre la misma cantidad. Esta cantidad supone lo que se conoce como la constante mágica del cuadrado. En este caso el resultado es 33, los años que, según la tradición, tenía Cristo cuando murió en la cruz.
Este es un ejemplo de matemáticas en el arte. Pero podemos encontrars muchos otros. Baste recordar las obras de Durero, Mondrian, Kandinsky, Tàpies, para encontrar abundantes referencias a números, relaciones geométricas, etc. En realidad podemos encontrar matemáticas en todos los aspectos de nuestra vida. Y también en Medicina. De esto hablaremos hoy.
Además, en el cuadrado mágico de la Sagrada Familia también se camufla una especie de firma subliminal, pues al sumar los números repetidos teniendo en cuenta el alfabeto romano obtenemos la sigla INRI, una abreviatura de Iesus Nazarenus Rex Iudeorum (Jesús de Nazaret, rey de los judíos) y se trata del rótulo que que según el evangelio Poncio Pilatos hizo escribir sobre la cruz de Jesucristo.
 |
| Una obra de Piet Mondrian: formas geométricas con colores primarios. |
Así, el ritmo reproductivo básico ( R0) es el número promedio de casos nuevos que genera un caso dado a lo largo de un período infeccioso. Esta métrica es útil debido a que ayuda a determinar cuando una enfermedad infecciosa puede dar lugar a un brote epidémico serio. Las raíces del concepto reproductivo básico se remonta al trabajo de Alfred Lotka, Ronald Ross y otros, aunque su primera aplicación moderna se debe a George MacDonald (1952), que construyó modelos epidemiológicos de la propagación del paludismo.
Cuando R0 < 1 la infección muere tras un largo período.
Pero si R0 > 1 la infección puede llegar a propagarse ampliamente entre una población.
Generalmente, cuanto más grande es R0 tanto más difícil será controlar la epidemia.
- Población susceptible (S), individuos sin inmunidad al agente infeccioso, y que por tanto puede ser infectada si es expuesta al agente infeccioso.
- Población infectada (I), indiviuos que están infectados en un momento dado y pueden transmitir la infección a individuos de la población suscpetible con la que entran en contacto.
- Población recuperada (R), individuos que son inmunes a la infección, y consecuentemente no afectan a la transmisión cuando entran en contacto con otros individuos. En este último término se incluyen tanto los que superan la enfermedad como los que fallecen por su causa.
La población total es N = S+I+R. El modelo relaciona las variaciones las tres poblaciones (Susceptible, Infectada y Recuperada) a través de la tasa de infección y el período infeccioso promedio: es la tasa de infección y γ coincide con la extensión del período infeccioso. A partir de aquí se pueden plantear ecuaciones que describan la variación temporal del número de individuos en cada compartimento y poder así analizar y predecir la evolución de la epidemia en el tiempo.
El modelo relaciona las variaciones las tres poblaciones (Susceptible, Infectada y Recuperada) a través de la tasa de infección y el período infeccioso promedio.
Pero esto lo explica mucho mejor un matemático:
La estadística es pues de gran ayuda para establecer predicciones en el curso de las epidemias. Aunque hay que tener en cuenta que los modelos matemáticos no son suficientes por si solos para valorar el origen y extensión de una epidemia. Como observa reiteradamente la Organización Mundial de la Salud (OMS), la recogida fiable, y el tratamiento adecuado de datos es fundamental para extraer conclusiones correctas.
Modelo de Kermack-Mckendrick Autores: Claudia Casaos y Carlos Guraieb:
Le matematiche delle epidemie: Il modello SIR


No hay comentarios:
Publicar un comentario